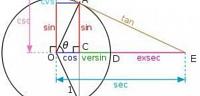
حساب المثلثات
حساب المثلثات (trigonometric) واحدا من فروع علم الهندسة العامة والذي بدوره فرع من فرةع الرياضيات الرئيسية ،التي تعنى بدراسة الزوايا والمثلثات وقيم المثلثية منها الجيب والجيب التمام، ويعد المصريين القدامى هم أول من عرفوا قواعد حساب المثلثات، والتي وظفوها أثناء بناء الأهرامات المصرية الثلاثة والمعابد المصرية القديمة، لكن ما تم توارثه عنهم هي المخطوطات التي دون بها، ومن خلال المخططات ظهر جليا أنهم عرفوا مساحة الدائرة ومساحة المربع، وتعود معرفتنا بعلم حساب المثلثات إلى الإغريقيين فهم من وضعوا قوانينها، ومن أهم ما وضعه الإغريقيين هي مفاهيم الزاوية القائمة والزاوية الحادة والزاوية المنفرجة.
تطبيقات علم المثلثات
من أهم التطبيقات في علم المثلثات حساب الزوايا والمسافات فيما يلي:
- أثناء إنشاء المباني والطرق.
- توظف في صناعة المحركات.
- تستخدم في تصنيع أجهزة التلفزيون والأثاث وملاعب الكرة.
- حساب المسافات الجغرافية بين القارات والدول والمدن.
- تستخدم في علم الفلك، وأنظمة الاستكشاف بالأقمار الصناعية.
قوانين حساب المثلثات
فيما يلي نضع بين أيديكم ملخصا لجميع قوانين حساب المثلثات التي قد نتطرق ووسائل لها في حياتنا العلمية والعملية وهي على النحو التالي:
- جا (س)= المقابل/الوتر.
- جتا (س)= المجاور/الوتر.
- ظا (س)= جا (س)/جتا (س).
- ظتا (س)= 1/ظا(س).
- ظتا (س)= جتا(س)/ جا(س).
- قا (س)= 1/ جتا(س).
- قتا (س)= 1/ جا (س).
- جا^2 (س)+جتا^2 (س)= 1.
- قا^2 (س)= 1+ظا^2 (س).
- قتا^2 (س)=1+ظتا^2 (س).
- جا (- س)=-جا (س).
- جتا (- س)= جتا (س).
- ظا (- س)=-ظا (س).
- جا (90-س)= جتا (س).
- جتا (90-س)= جا (س).
- ظا (90-س)= ظتا (س).
- جا (90+س)= جتا (س).
- جتا (90+س)=-جا (س)
- ظا (90+س)=-ظتا (س).
- جا (180-س)= جا (س).
- جتا (180-س)=-جتا (س).
- ظا (180-س)=-ظا (س).
- جا (180+س)=-جا (س).
- جتا (180+س)=-جتا (س).
- ظا (180+س)= ظا (س).
- جا (360-س)=-جا (س).
- جتا (360-س)= جتا (س).
- ظا (360-س)=-ظا (س).
- جا (360+س)= جا (س).
- جتا (360+س)= جتا (س).
- ظا (360+س)= ظا (س).
- جا (أ+ب)= جا (أ) جتا (ب)+جتا (أ) جا (ب).
- جا (أ-ب)= جا (أ) جتا (ب)-جتا (أ) جا (ب).
- جتا (أ+ب)= جتا (أ) جتا (ب)-جا (أ) جا (ب).
- جتا (أ-ب)= جتا (أ) جتا(ب)+جا (أ) جا (ب).
- ظا (أ+ب)= (ظا (أ)+ظا(ب))/(1-(ظا(أ)ظا(ب))).
- ظا (أ-ب)= ((ظا (أ)-ظا(ب))/(1+ ظا (أ) ظا (ب)).
- جا (أ+ب) جا (أ-ب)= جا^2 (أ)-جا^2 (ب)= جتا^2 (ب)-جتا^2 (أ).
- جتا (أ+ب) جتا(أ-ب)= جتا^2 (أ)-جا^2(ب)= جتا^2 (ب)-جا^2 (أ).
- ظا (45+أ)= (1+ظا (أ))/(1- ظا (أ)).
- ظا (45-أ)= (1- ظا (أ))/(1+ظا(أ)).
- 2جا (أ) جتا (ب)= جا (أ+ب)+جا ( أ-ب).
- 2جتا (أ) جا (ب)= جا (أ+ب)-جا (أ-ب).
- 2جتا (أ) جتا (ب)= جتا (أ+ب)+جتا (أ-ب).
- 2جا (أ) جا (ب)= جتا (أ-ب)-جتا (أ+ب).