جدول المحتويات
المثلث
المثلث هو أحد الأشكال الهندسية المشهورة بجانب المربع و الدائرة و المستطيل ، و المثلث شكل هندسي يتكون من ثلاثة أضلاع فقط و ثلاث زوايا ، و المثلثات بالعادة تتواجد على أكثر من شكل و الذي يتحكم بشكل هو الزاوية و طول الضلع نذكر أن هناك ثلاثة أنواع من المثلثات و تطبق قاعدة واحدة في قياس مساحة المثلث .
أنواع المثلثات
- مثلث قائم الزاوية ، أي مثلث فيه زاوية واحدة قياسها 90 درجة و طول ضلعها أطول من الأضلاع الأخرى .
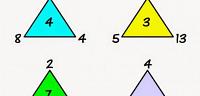
- مثلث متساوي الساقين ، و هو مثلث يوجد به ضلعين متساوي الطول و له و زاويا الضلعين أيضاً لها القياس نفسه.
- مثلث متساوي الأضلاع ، و هو مثلث كل أضلاعه متساوية الطول و كل زواياه متشابهة القياس أي له القياس نفسه .
قانون حساب مساحة المثلث
هناك قاعدة مشهورة لحساب مساحة المثلث و تطبق على كافة المثلثات و هي :
- مساحة المثلث = نصف طول القاعدة × الإرتفاع
- مساحة المثلث = (طول القاعدة × الإرتفاع ) ÷ 2
- مساحة مثلث قائم الزاوية = طول ضلعي الزاوية القائمة ÷ 2
أمثلة على حساب مساحة المثلث
- المثال الأول :مثلث متساوي الساقين طول ضلعه 8 سم و طول قاعدته 8 و طول ارتفاعه 8 سم ، ما مساحة المثلث ؟
- على قانون مساحة المثلث : مساحة المثلث = نصف طول القاعدة × الإرتفاع
= 4 × 8 = 32 سم 2
- مساحة المثلث = (طول القاعدة × الإرتفاع ) ÷ 2
= 8×8 =64 ÷2 =32 سم مربع
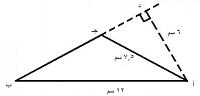
- المثال الثاني مثلث قائم الزاوية طول الضلع القائم يساوي 8 سم و طول قاعدة الضلع القائم يساوي 8 سم ، إحسب مساحة المثلث ؟
- مساحة مثلث قائم الزاوية = طول ضلعي الزاوية القائمة ÷ 2
= طول ضلع القائمة × طول ضلع قاعدة القائم ÷ 2 = 8×8 = 64 ÷ 2 = 32 سم مربع ملاحظة في المثلث القائم الزاوية عندما يكون أحد طول الأضلاع مجهول نجد قيمة المجهول على قانون فيثاغورس وهو مربع طول الوتر = مربع طول الضلع الأول القائم + مربع طول الضلع الثاني القائم
- المثال الثالث مثلث متساوي الأضلاع طول أحد أضلاعه يساوي 8 سم و طول إرتفاعه 8 سم ،احسب مساحة المثلث؟
= (8×8) ÷ 2 = 64 ÷ 2 = 32 سم مربع