قانون محيط المثلث
للمثلث قوانين كثيرة في علم الرياضيات باختلاف أنواعه، والتي يسأل كثيرا عنها، وعن حساباتها، ولا يستغنى عنها في الحياة اليومية والعملية، وتدرس هذه القوانين في الصفوف الدراسية على أنها من أساسيات الرياضيات.
تعريف ومعنى ومعنى المثلث
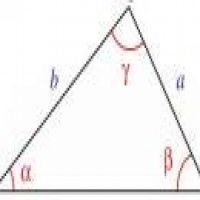
ويعرف المثلث: بأنه منظومة هندسية اخترعها العالم باسكال، وهو مجموعة من الرؤوس التي تربط بينها قطع مستقيمة، وهذه القطع المستقيمة تسمى أضلاعا، وأهم خاصية يعرف بها المثلث أن مجموع زواياه يساوي 180، وثاني أهم خاصية أن مجموع طولي ضلعيه الأصغرين أكبر من طول الضلع الأكبر.
أنواع المثلثات
للمثلث أنواع متعددة، ولكل نوع خصائص ومميزات وهيئة تختلف عن النوع الآخر، وتصنف أنواع المثلثات حسب الأضلاع تارة، وحسب الزوايا تارة أخرى، أما أنواع المثلثات حسب الزوايا فهي ثلاثة أنواع:
- المثلث قائم الزاوية: ويمتاز هذا النوع من المثلثات بأنه يحتوي زاوية قائمة مقياسها 90 درجة، ومجموع الزاويتين الباقيتين يساوي 90 درجة، وهو الأشهر بين التلاميذ وطلبة العلم؛ لسهولة قوانينه والتعامل معه.
- المثلث حاد الزاوية: ويمتاز هذا النوع من الزوايا أن جميع زواياه أقل من 90 درجة، ويجد بعض الطلبة صعوبة في تمييز شكله.
- المثلث منفرج الزاوية: ويمتاز هذا المثلث بوجود زاوية فيه مقياسها أكبر من 90 درجة، وأقل من 180 درجة، ويجد الطلاب سهولة في تمييزه من خلال هذه الزاوية شديدة الانفراج.
أما أنواع المثلثات حسب أطوال أضلاعها، فهي ثلاثة أنواع، منها:
- المثلث المتساوي الأضلاع: ويمتاز هذا المثلث بتساوي أضلاعه الثلاثة، أي جميع أضلاعه تحمل القياس نفسه، وبالتالي تساوي جميع زواياه التي تحمل قياس 60 درجة.
- المثلث المتساوي الساقين: أو بما يعرف متساوي الضلعين، ويتميز هذا المثلث بتساوي ضلعين يحملان القياس نفسه، وبالتالي الزوايا المقابلة للضلعين المتساويين متساويتين.
- المثلث المختلف الأضلاع، وهذا الأكثر انتشارا والأكثر طبيقا لجميع القوانين المثلثية، وهو يتميز باختلاف أضلاعه واختلاف زواياه.
محيط المثلث
حساب محيط المثلث من أسهل الحسابات التي تجري على المثلث، فالمحيط ببساطة هو: مجموع أطوال أضلاع المثلث، ومن الواجب معرفة ما هى طريقة عمل الأطوال، وفي حال عدم وجود قيمة للضلع بشكل مباشر، يشار إلى قيمتها بطريقة أو أخرى كذكر خاصية من خصائص المثلث على سبيل المثال، ومن الجدير ذكره أن في حالة اختلاف الوحدات الخاصة بأطوال الأضلاع يجب تحويلها وتوحيدها، ومن ثم اجمع الضلع الأول، مع الضلع الثاني والثالث، فينتج محيط المثلث، ولا ننسى أن كتابة القانون أولا ومن ثم ترتيب الأرقام تحته، لضمان الحصول على إجابة صحيحة.