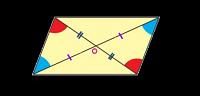
متوازي الأضلاع
هو شكلٌ رباعيٌ هندسيٌ منتظم فيه كلّ ضلعين متقابلين متوازيين ومتساويين في الطّول، وكل زاويتين متقابلتين متساويتين، وقطراه ينصفان بعضهما البعض، ومجموع قياس زواياه يساوي ثلاثمائة وستين درجة، وهو حالة شبيهة بالمعين، ويمكن القول من هذا التعريف ومعنى بأنّ المربع والمستطيل والمعين حالاتٌ خاصّة من متوازي الأضلاع.
خصائص متوازي الأضلاع
- كل زاويتين متقابلتين متساويتين في القياس، وكل زاويتين متجاورتين للضلع نفسه مجموع قياسهما يساوي مائة وثمانين درجة.
- كل ضلعين متقابلين متطابقين متساويين، وكل قطر في الشّكل الرُباعي هو منصف للآخر، وتُسمى نقطة تقاطع القطرين بمركز متوازي الأضلاع، وأي مستقيم يمر بهذه النّقطة يقسم متوازي الأضلاع إلى نصفين متطابقين في القياس.
- مساحة متوازي الأضلاع تساوي ضعف مساحة المثلث المتشكّل بضلعين وقطر، وسنتعرّف معاً على طريقة حساب مساحة هذا الشّكل.
- إذا تعامد قطرا متوازي الأضلاع وتساوى فيه كلّ ضلعين متجاورين في القياس يكون الشّكل معيناً.
- إذا تساوى قطرا متوازي الأضلاع وإحدى زواياه قائمة يكون الشّكل مستطيل، وإذا انطبقت كلا حالتي المعين والمستطيل معاً في الشّكل الرباعي يكون الشكل مربع.
قانون مساحة متوازي الأضلاع
مساحة متوازي الأضلاع بدلالة القاعدة
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع
مثال:
أوجد مساحة متوازي الأضلاع إذا علمت أنّ طول أحد أضلاعه 5 سم، وطول العامود النّازل على القاعدة يساوي 6 سم.
الحل:
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع. =5×6 =30 سم2
مساحة متوازي الأضلاع بدلالة الزاوية
يمكن احتساب مساحة متوازي الأضلاع بقياس أي زاوية فيه ومعرفة قياس طول كلّ ضلعين متجاورين، أي
مساحة متوازي الأضلاع = طول الضلع الأول (a) × طول الضلع الثاني الذي يجاوره (b)× جيب الزاوية (sin)
مثال:
أوجد مساحة متوازي الأضلاع إذا علمت أنّ طول أحد أضلاعه 16سم، وطول الضلع الذي يجاوره هو 7سم، وقياس الزاوية الذي تجاوره الضلع الأول هي 60 درجة.
الحل:
على القانون أعلاه، بداية نجد جيب الزاوية 60 من خلال الآلة الحاسبة وتساوي تحت الجذر 3÷2.
مساحة متوازي الأضلاع = (a) × (b)× جيب الزاوية. = 16×7× ? 3÷2 =8×7×? 3 =56? 3سم2 .
مساحة متوازي الأضلاع بدلالة مساحة المثلث
يمكن حساب مساحة متوازي الأضلاع بمعرفة قياس طول القطرين وقياس الزاوية المحصورة بينهما، وسنتستخدم هنا قانون مساحة المثلث.
مساحة متوازي الأضلاع = 2× مساحة المثلث.( ضعف مساحة المثلث). = 2×( ½ ×طول القاعدة ×الارتفاع)
ويساوي أيضاً. مساحة متوازي الأضلاع = 2× مساحة المثلث
=2× ( ½ ×طول الضلع الأول×اطول الضلع الثاني ×جيب الزاوية المحصورة بينهما.)
أمثلة على حساب مساحة متوازي الأضلاع
لوح خشبي على شكل متوازي أضلاع مساحته تساوي مساحة مربع طول ضلعه 13 سم، احسب طول قاعدة متوازي الأضلاع إذا علمت أنّ طول ارتفاعه 10 سم؟
الحل:
مساحة متوازي الأضلاع تساوي مساحة المربع ( طول الضلع×طول الضلع)=(13×13)=169سم2.
مساحة متوازي الأضلاع = طول القاعدة × الارتفاع. 169 = س × 10 س= 169÷10 فطول القاعدة يساوي 16.9سم.