خصائص المربع .
المضلعات الرباعية متنوعة منها المربع و المعين و متوازي الاضلاع و شبه المنحرف فمتى نقول ان المضلع الرباعي مستطيل ؟
هناك بعض الخصائص التي اذا توافرت كان الشكل الرباعي عبارة عن مستطيل تتمثل في : –
1- كل زواياه متساوية و قياس كل زواية يساوي 90 درجة اي ان كل زواياه قائمة .
2- كل ضلعين فيه متقابلين متساويين و متوازيين .
3- قطراخ متساويان في الطول و ينصف كل منهما الآخر .
4- المستطيل له محوري تماثل فقط .
5- كل قطر من اقطار المستطيل يقسمه الى مثلثين متطابقين .

يسمى الضلع الاطول في المستطيل طول المستطيل و الاقل طولًا هو العرض , يلاحظ ان اضلاعه الاربع فيه الضلعين الاطول الممثلان للطول متقابلان و نجدهما متساويين و متوازيين و كذلك الضلعين الاقصر اذ كما عرفنا فانه مضلع رباعي اي يتكون من اربع حروف او اربع اضلاع .

كيف تحسب مساحة المستطيل ؟
الطريقة الاولى .
لحساب مساحة المستطيل هناك معادلة اساسية من خلالها يتم حساب مساحتة و هى : –
مساحة المستطيل = الطول ( ل ) X العرض ( ع ) و الناتج يحسب بالسم المربع او المتربع او ايًا كانت ودة القياس المستخدمة المهم ان وحدة قياس المساحة هى التربيع .
مثال : – مستطيل طوله يساوي 10 سم و عرضه يساوي 7 سم اوجد مساحة المستطيل .
الحل .
مساحة المستطيل = ل X ع = 10 X 7 = 70 سم2
و من خلال هذا القانون تستطيع الحصول على الطول او العرض بقوانين متفرعة منه و لكن هنا يجب ان يكون بالمعادلة مجهول واحد اي انه للحصول على طول المستطيل يكون معطى لنا العرض و المساحة او العكس .
الطول ( ل ) = المساحة العرض ( ع )
العرض ( ع ) = المساحة الطول ( ل )
مثال : – مستطيل مساحته 72سم2 و طوله يساوي 12 سم او جد عرضة .
الحل .
ع = المساحة الطول = 7212 = 6 سم
مثال : – مستطيل مساحته 36 سم2 و عرضه يساوي 4 سم احسب طوله .
الحل .
ل = 364 = 9 سم

الطريقة الثانية .
تطبيق نظرية فيثاغورث عندما يكون معلوم لديك طول احد اجناب المستطيل و قطره هنا تستطيع تطبيق نظرية فيثاغورث للحصول على الحد الثاني , من المعروف انه من خواص المستطيل ان كل زواياه الاربع قوائم اي ان كل زاوية يحدها ضلعين من اضلاع المستطيل احدهما يكون الطول و الآخر العرض هما ضلعي الزاوية القائمة او ما نطلق عليه ضلعي القائمة و القطر هنا يمثل الوتر او الضلع المقابل للزاوية القائمة , لذا فانه يمكن تطبيق نظرية فيثاغورث الخاصة بالمثلث القائم الزاوية و تساعدنا في الحصول على ايًا من ضلعي القائمة او حرفي المستطيل بمعلومية الضلع الثاني و الوتر .
معادلة نظرية فيثاغورث .
مربع طول الوتر = مجموع مربعي ضلعي القائمة .
في حال المستطيل .
مربع القطر = مرع الطول + مربع العرض .
القوانين الفرعية .
الطول = الجذر التربيعي لمربع القطر – مربع العرض .
العرض = الجذر التربيعي لمربع القطر – مربع الطول .
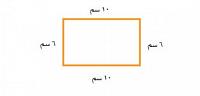
مثال : – مستطيل طول قره 10 سم و عرضه يساوي 6 سم احسب مساحة المستطيل .
الحل .
طول المستطيل = الجذر التربيعي لمربع القطر – مربع العرض
= الجذر التربيعي لـ 100 – 36
= الجذر التربيعي لـ 64 = 8 سم .
مساحة المستطيل = الطول X العرض = 6 X 8 = 48سم2
مثال : – مستطيل طول قطره 5 سم و طوله يساوي 4 سم اوجد مساحته .
الحل .
عرض المستطيل = الجذر التربيعي لمربع القطر- مربع الطول .
= الجذر التربيعي لـ 25 – 16
= الجذر التربيعي لـ 9 = 3سم .
مساحة المستطيل = الطول X العرض = 3 X 4 = 12 سم2 .

المستطيل هو أحد الأشكال الهندسية المهمّة في مجالات العلوم التطبيقيّة والهندسية، فهو شكل رباعي ثنائي البعد، له أربعة زوايا قائمة قياسها 90 درجة مئوية، وأربعة أضلاع متعامدة بحيث إنّ كلّ زوجين من متقابلين متساويين، من أبرز حالات المستطيل الخاصّة المربّع، أي أنّ المربع هو مستطيل تتساوى جميع أضلاعه، كما يعتبر المستطيل حالة خاصّة من متوازي الأضلاع.

آ 

خصائص المستطيل

نقول عن شكل رباعي أنّه مستطيل إذا تحققت فيه الشروط التالية:

• إذا كانت جميع زواياه تساوي بعضها البعض.
• إذا كان متوازي أضلاع وتساوى فيه قطراه وكانت إحدى زواياه قائمة.
• إذا كان متوازي أضلاع (أ ب ج د) وكان المثلثان (أ ب ج) و(ج د أ) يطابق كلٌ منهما الآخر.

آ 

قوانين المستطيل

بما أنّ المستطيل شكل ثنائي البعد يمتاز بأنّ له بعدين هما العرض والطول، إذن يمكن حساب محيطه من المعلومات المعروفة لدى الجميع عن المضلعات المنتظمة الرباعية، وبالتالي فإنّ محيطه هو عبارة عن مجموع أطوال أضلاعه، وبصيغة رياضية يُكتب قانون محيطه كما يلي:

محيط المستطيل=مجموع أطوال أضلاعه

محيط المستطيل=2×(الطول+العرض)

أما عن قانون مساحته فإنّها تساوي حاصل ضرب طوله في عرضه، وبصيغة رياضية تُمَثَّل كما يلي:

مساحة المستطيل=الطول×العرض

آ 

أمثلة توضيحية

مثال 1آ :

بنى عامل بناء بيت على شكل مستطيل، طوله 8م وعرضه 6م، ما هي مساحة البيت ومقدار محيطه؟

الحلآ :

مساحة المستطيل=الطول×العرض

مساحة المستطيل=8 م×6م

مساحة المستطيل=48م2

مساحة البيت=48م2.

آ 

محيط المستطيل=(2×الطول+العرض)

محيط المستطيل=(2×8 م+6 م)

محيط المستطيل=(2×14م)

محيط المستطيل=28م

محيط البيت=28م

مثال 2آ :

بركة سباحة مستطيلة الشكل محيطها 50م وعرضها 10م، ما هي مساحتها؟

الحلآ :

نجد طول البركة باستخدام قانون محيط المستطيل

محيط المستطيل=2×(الطول+العرض)

50 م=2×(الطول+10م)

50 م / 2=الطول+10م

25 م-10 م=الطول

15م=الطول

طول البركة=15م.

آ 

نجد مساحة البركة باستخدام قانون مساحة المستطيل

مساحة المستطيل=الطول×العرض

مساحة المستطيل=15م× 10م

مساحة المستطيل=150م2

مساحة البركة=150 م2.

مثال 3آ :

إذا كان محيط حديقة مستطيلة الشكل هو 48 م ومساحتها 40م2، ما هو طولها وعرضها؟

الحلّ:

نفرض أنّ طول الحديقة=س

نفرض أن ّعرض الحديقة=ص

من قانون محيط المستطيل نستنتج المعادلة الأولى وهي كما يلي:

محيط المستطيل=2×(الطول+العرض)

48=2×(س+ص)

48 / 2=س+ص

14= س+ص

14-ص=س

من قانون مساحة المستطيل نستنتج المعادلة الثانية، وهي كما يلي:

مساحة المستطيل=الطول×العرض

40=س×ص

40 / ص=س

بتعويض المعادلة الثانية في المعادلة الأولى:

14-ص=(40 / ص)

14ص-(ص2)=40

14ص-(ص2)-40=0

نضرب المعادلة في المقدار (-1)

(ص2)-14ص+40=0

نحلل المعادلة التربيعية لإيجاد قيمة ص:

(ص-4) (ص-10)=0

ص-4=0 أو ص-10=0

ص=4 أو ص=10

نستنتج أن عرض المستطيل يمكن أن يكون 4 أو م10.

لإيجاد قيمة طول المستطيل نعوض في المعادلة الأولى قيم عرض المستطيل:

14-ص=س

14-10=4

أو

14-4=10

بما أنّ طول الضلع الأكبر في المستطيل يمثل الطول إذن طوله=10م وعرضه=4م.

قوانين مساحة المربّع

تُعرّف مساحة المربع على أنها تلك المنطقة التي تقع داخل حدوده، حيثُ تمثل حدود المربع الجوانب الأربعة المكونة له، كما تُعرف بأنّها مقدار المساحة التي يغطيها، وتُقاس عادة بالوحدات المربعة، ويتم حسابها باستخدام أحد القوانين الآتية:[ظ،][ظ¢]

• يمكن إيجاد مساحة المربع عند معرفة طول أحد أضلاعه باستخدام المعادلة الرياضية الآتية:
  • مساحة المربع = طول الضلع × طول الضلع؛ أي: مساحة المربع = (طول الضلع)2، وبالرموز:
  • م=س2؛ حيث:
    • م: مساحة المربع.
    • س: طول الضلع.
  • فمثلاً لإيجاد مساحة المربع الذي يبلغ طول ضلعه 6 أمتار يجب تعويض قيمة طول الضلع في المعادلة كالآتي: مساحة المربع = (6 م)2، ثم حساب الناتج: مساحة المربع = 36 م2.[ظ£]
• يُمكن حساب المساحة لمربع ما من خلال معرفة قيمة قطر ذلك المربع، وذلك باستخدام المعادلة الرياضية الآتية:
  • مساحة المربع = (طول القطر)2 ÷ 2، وبالرموز:
  • م=ق2÷ 2؛ حيث:
    • ق: طول قطر المربع.
  • فمثلاً لإيجاد مساحة مربع يبلغ طول قطره 10سم، يجب تعويض قيمة طول القطر في المعادلة كالآتي: مساحة المربع = (10سم)2 ÷ 2، ثم حساب الناتج كالآتي: مساحة المربع = 102 ÷ 2، أي أنّ مساحة المربع = 50سم2.[ظ¤]
• يُعرَف محيط المربع بأنّه إجمالي المسافة حول الشكل الخارجي للمربع، ويُمكن إيجاد المساحة لمربع ما إذا عُلم محيطه، وذلك من خلال قسمة قيمة المحيط على العدد 4، ليتمّ الحصول على قياس طول الضلع الواحد من أضلاع المربع، وعند معرفة طول ضلع المربع يُمكن استخدام قانون إيجاد مساحة المربع بدلالة طول ضلعه وهو: مساحة المربع = (طول الضلع)2 .[ظ،]

أمثلة متنوعة على كيفية إيجاد مساحة المربع

أمثلة على حساب المساحة باستخدام طول الضلع

• المثال الأول: جد مساحة المربع الذي يبلغ طول ضلعه 16سم.[ظ¥]
  • الحل: بتطبيق القانون: م=س2=162=256سم2.

• المثال الثاني: جد مساحة المربع الذي يبلغ طول ضلعه 0.6م.[ظ¦]
  • الحل: بتطبيق القانون: م=س2=0.62=0.36م2.

• المثال الثالث: جد طول ضلع المربع إذا كانت مساحته 529سم2.[ظ¥]
  • الحل: بتطبيق القانون: م=س2=529، ومنه س=23سم.

• المثال الرابع: إذا كانت هناك حديقة مربعة الشكل طول ضلعها 10سم، جد مساحتها.[ظ¦]
  • الحل: بتطبيق القانون: م=س2=102=100سم2.

• المثال الخامس: إذا أراد قصي فرش غرفته المربعة بالكامل بالسجاد، وكان طول ضلع غرفته 4م، جد مساحة السجاد التي يجب على قصي إحضارها.[ظ¦]
  • الحل: بتطبيق القانون: م=س2=42=16م2؛ أي عليه إحضار سجادة مساحتها 16م2.

• المثال السادس: إذا كان طول ضلع أحد الحقول 275م، جد تكلفة حرثه إذا كانت 0.06 دينار لكل متر مربع.[ظ§]
  • الحل:
    • حساب مساحة الأرض أولاً لحساب التكلفة بتطبيق القانون: م=س2=2752=75625 م2.
    • حساب التكلفة عن طريق ضرب مساحة الأرض بتكلفة حراثتها، أي تكلفة الحراثة= 0.06×75,625= 4537.5 دينار.

• المثال السابع: إذا تمت زيادة طول كل ضلع من أضلاع المربع 2سم، وازدادت مساحته نتيجة لذلك 44سم2، جد طول أضلاع المربع قبل الزيادة.[ظ¨]
  • الحل: نفترض أن س هو طول ضلع المربع قبل الزيادة، وم هي مساحته قبل الزيادة، وعليه م=س2، أما المساحة بعد الزيادة فهي م 44=(س 2)2، وبتعويض بقيمة م في المعادلة الثانية ينتج أن: س2 44=(س 2)2، ومنه س=10سم، أي أن طول ضلع المربع قبل الزيادة =10سم.

• المثال الثامنآ : في المربع (أب ج د)، كانت النقطة (ه) منتصف الضلع أب، والنقطة (و) منتصف الضلع ب ج، والنقطة (ز) منتصف الضلع ج د، والنقطة (ح) منتصف الضلع أد، وقاعدته هي (دج)، تم الوصل بين هذه النقاط بخطوط مستقيمة لتشكيل المربع الداخلي ( ه وزح) داخل المربع (أب ج د)، كم النسبة بين مساحتي هذين المربعين.[ظ¦]
  • الحل:
    • نفترض أن (س) هو طول ضلع المربع المربع الكبير (أب ج د)، وعليه فإن مساحته= م=س2.
    • إيجاد طول ضلع المربع الداخلي بعد تطبيق نظرية فيثاغورس على أحد المثلثات المحصورة بين المربعين مثل المثلث (أه ح): (ه ح)2= (أح) 2 (أه) 2، (ه ح)2=(س/2)2 (س/2)2، ومنه (ه ح)= 2âˆ?/س؛ أي أن طول ضلع المربع الداخلي (ه وزح)= 2âˆ?/ س.
    • مساحة المربع الداخلي= م=2/س2 .
    • حساب النسبة بين مساحة المربعي عن طريق قسمة مساحة المربع الكبير على مساحة المربع الصغير=(2/س²)/س²=2